Code

The code for most papers is available on Github.

Self-supervised learning with rotation-invariant kernels

Code: available here.

If you use this toolbox, please cite the following paper: “Self-supervised learning with rotation-invariant kernels”, L. Zheng, G. Puy, E. Riccietti, P. Pérez, R. Gribonval, International Conference on Learning Representations (ICLR), 2023.

Link to paper.

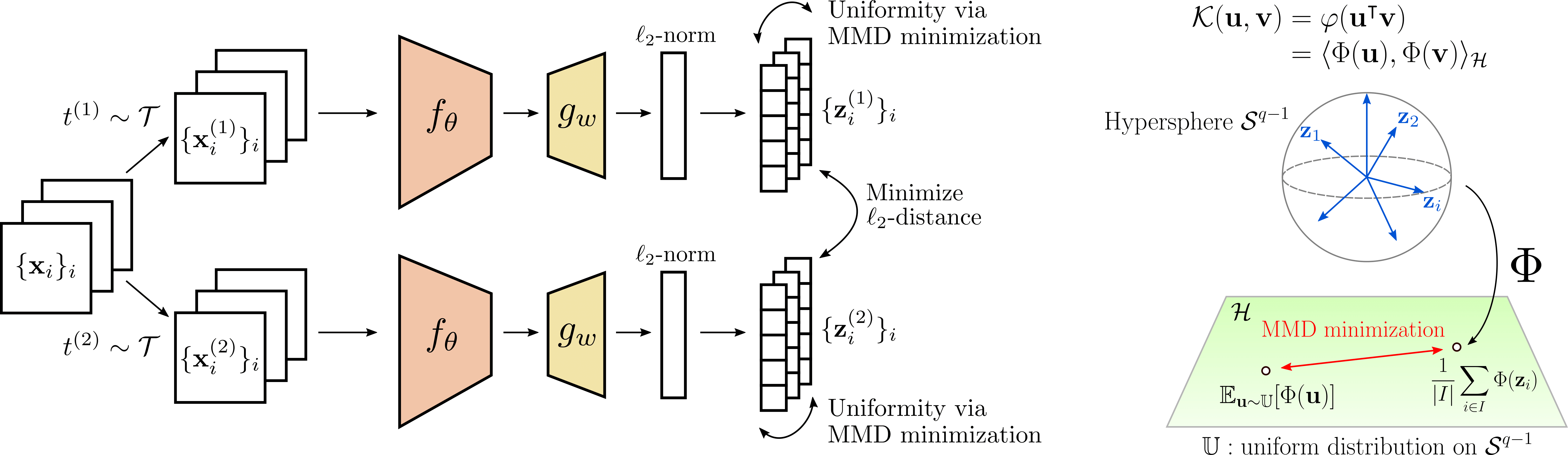
Abstract: We introduce a regularization loss based on kernel mean embeddings with rotation-invariant kernels on the hypersphere (also known as dot-product kernels) for self-supervised learning of image representations. Besides being fully competitive with the state of the art, our method significantly reduces time and memory complexity for self-supervised training, making it implementable for very large embedding dimensions on existing devices and more easily adjustable than previous methods to settings with limited resources. Our work follows the major paradigm where the model learns to be invariant to some predefined image transformations (cropping, blurring, color jittering, etc.), while avoiding a degenerate solution by regularizing the embedding distribution. Our particular contribution is to propose a loss family promoting the embedding distribution to be close to the uniform distribution on the hypersphere, with respect to the maximum mean discrepancy pseudometric. We demonstrate that this family encompasses several regularizers of former methods, including uniformity-based and information-maximization methods, which are variants of our flexible regularization loss with different kernels. Beyond its practical consequences for state-of-the-art self-supervised learning with limited resources, the proposed generic regularization approach opens perspectives to leverage more widely the literature on kernel methods in order to improve self-supervised learning methods.

Butterfly sparse matrix factorization

Efficient identification of butterfly sparse matrix factorization.

Code: available here.

If you use this toolbox, please cite the following paper: “Efficient Identification of Butterfly Sparse Matrix Factorizations”, L. Zheng, E. Riccietti, R. Gribonval, SIAM Journal on Mathematics of Data Science, 5(1), 22-49., 2023.

Link to paper.

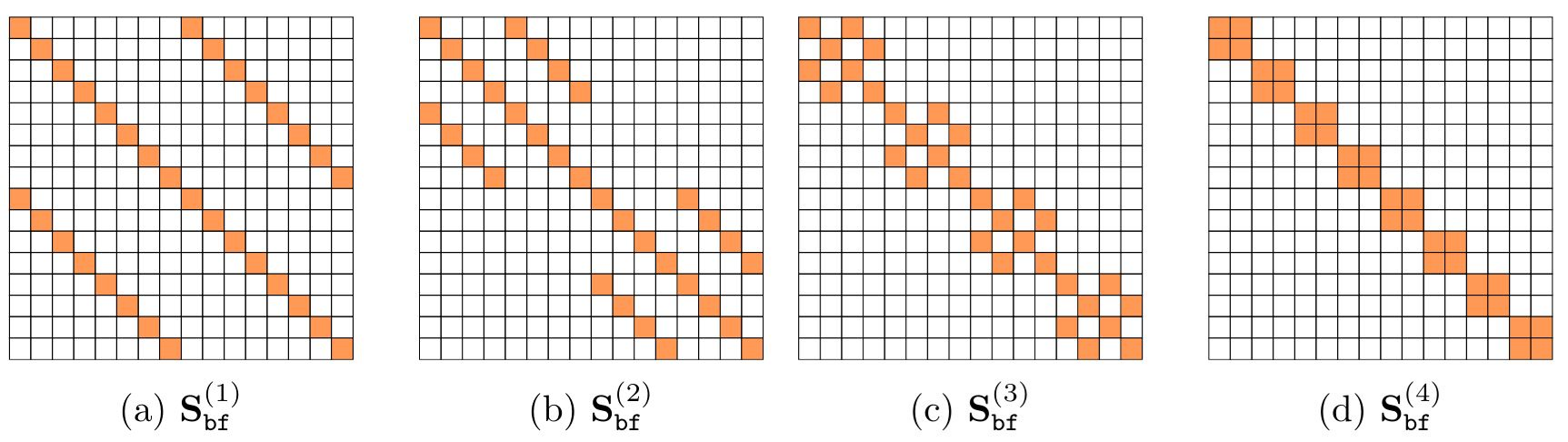
Abstract: Fast transforms correspond to factorizations of the form $Z=X^{(1)} … X^{(J)}$, where each factor $X^{(\ell)}$ is sparse and possibly structured. This paper investigates essential uniqueness of such factorizations, i.e., uniqueness up to unavoidable scaling ambiguities. Our main contribution is to prove that any N×N matrix having the so-called butterfly structure admits an essentially unique factorization into J butterfly factors (where $N=2^J$), and that the factors can be recovered by a hierarchical factorization method, which consists in recursively factorizing the considered matrix into two factors. This hierarchical identifiability property relies on a simple identifiability condition in the two-layer and fixed-support setting. This approach contrasts with existing ones that fit the product of butterfly factors to a given matrix via gradient descent. The proposed method can be applied in particular to retrieve the factorization of the Hadamard or the discrete Fourier transform matrices of size $N=2^J$. Computing such factorizations costs $O(N^2)$, which is of the order of dense matrix-vector multiplication, while the obtained factorizations enable fast $O(N \log N)$ matrix-vector multiplications and have the potential to be applied to compress deep neural networks.

Fast learning of fast transforms, with guarantees.

Code: available here.

If you use this toolbox, please cite the following paper: “Fast learning of fast transforms, with guarantees”, Q. T. Le, L. Zheng, E. Riccietti, R. Gribonval, IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2022.

Link to paper.

Abstract: Approximating a matrix by a product of few sparse factors whose supports possess the butterfly structure, which is common to many fast transforms, is key to learn fast transforms and speed up algorithms for inverse problems. We introduce a hierarchical approach that recursively factorizes the considered matrix into two factors. Using recent advances on the well-posedness and tractability of the two-factor fixed- support sparse matrix factorization problem, the proposed algorithm is endowed with exact recovery guarantees. Experiments show that speed and accuracy of the factorization can be jointly improved by several orders of magnitude, compared to gradient-based optimization methods.